Word Rotator’s Distance
Word Rotator’s Distance とは
2つの自然言語文あるいは文書が与えられたとき,それらの(非)類似度を測る尺度として Word Mover’s Distance (WMD)*1と呼ばれる手法が提案されている。 これは文を構成する単語ベクトルのアラインメントを最適輸送コストに基づき計算することで,文間の(非)類似度を見積もる手法である。 WMDの解説は下記が詳しい。 yubessy.hatenablog.com
WMDはgensimに実装がありすぐに使える。
gensim.models.Word2Vec.wmdistance
Word Rotator’s Distance(WRD)は,このWMDの改良版であり2020年に横井らにより提案された*2。
多くの先行研究や観測事実を鋭い洞察力で整理し,合理的でシンプルなアイデアでありながらも誰も思いつかなかったのを最初にやったという意味ではすごい(小並感)。 実装コストもほぼ無で計算機パワーも手持ちのラップトップで十分という,個人的にはこういう研究がとても好み。
閑話休題。
さて,自分語りはキモいのでここまでとして, WRDのポイントを一言でいうとWMDでは単語の意味と重要度を混ぜて計算していたのをWRDではそれらを分離して性能向上しましたよという話である。 詳細は横井らの論文を読んでほしい。arXiv版がより詳しいが, さくっと日本語で概要を掴みたい人は人工知能学会版*3もしくは言語処理学会版*4の予稿を読むと良い。
実装
最適輸送の実装は論文にも書いてある通りPythonの最適輸送ライブラリであるPOTを使うとよい。関数をコールするだけである。
POT: Python Optimal Transport — POT Python Optimal Transport 0.7.0 documentation
最適輸送の計算に必要なのは,2つの確率分布とコスト行列である。 確率分布が文ベクトル,コスト行列が文を構成する単語ベクトル間の非類似度に対応する。 WRDでは,文ベクトルの各要素を各単語ベクトルのノルムで重み付けし正規化する。また単語ベクトル間の非類似度としてコサイン距離を使う。 WMDでは,この重みが一様分布であり,非類似度がL2ノルムだったのである。 詳細はarXiv版のAlgorithm1にあるのでそれを書くだけ。冗長に書けば例えば下記。
import numpy as np from sklearn.preprocessing import normalize import ot def wrd(s, sp): w_norm = np.linalg.norm(s, ord=2, axis=1) wp_norm = np.linalg.norm(sp, ord=2, axis=1) ms = w_norm/np.sum(w_norm) msp = wp_norm/np.sum(wp_norm) s_norm = normalize(s, norm='l2', axis=1, copy=False) sp_norm = normalize(sp, norm='l2', axis=1, copy=False) C = 1 - s_norm @ sp_norm.T Wd = ot.emd2(ms, msp, C) return Wd
全体のコードは整理したらGitHubで公開する。
実験
論文ではSTS-B(dev)で評価しているので同じデータセットを使う。 ここからダウンロードできる。
単語ベクトルは手元にあったglove.6B.100d.txtを使った。 ここからダウンロードできる。
結果
stopwordsの除去有無での Pearson' ρ は以下の通り。 stopwordsはnltkのをそのまま適用した。
除去あり: 0.71247
除去なし: 0.62859
微妙に違うけど論文のTable.6の結果のような数字が出た。
なお,未知語は除去しWRDのスコアはSTS-Bの人手スコアとは逆センスなので-1倍した。
次やること
単語ベクトルの各種後処理(VC)をかましてみる。
私からは以上です。
ランダム行列の固有値の円則
昨日に引き続き、数セミ2019年2月号から。

- 出版社/メーカー: 日本評論社
- 発売日: 2019/01/12
- メディア: 雑誌
- この商品を含むブログを見る
今日は白井朋之さん(九州大学IMI)の記事「ランダム行列から行列式点過程へ」から。 昨日はGUEを考えたが、今回はもう少し一般的なランダム行列であるGinibreランダム行列を考える。 数セミでは、まずGinibreランダム行列を定義し、GUEはこれの特殊形になっていることを示す。 そのあと、固有値分布がどうなっているか調べる。
以下に概略を書いておく。
Ginibreランダム行列
複素確率変数\( Z \)の確率密度関数が、 \begin{align} f(z) = \pi^{-1} e^{-|z|^2} ,(z \in \mathbb{C}) \end{align} のときに、\( Z \)は複素標準正規分布\( Z \)に従う。すなわち、\( Z \sim N_{\mathbb{C}}(0,1) \)。
\( Z = X + iY\)と書くと、\( X, Y \overset{i.i.d.}{\sim } N_{\mathbb{R}}(0, \frac{1}{\sqrt{2}} )\)1。
で、Ginibreランダム行列とは、各成分が上記の複素確率変数\(Z\)のランダム行列のこと。 すなわち、それを\(G\)とし、行列サイズを\(p \times p\)とすると以下の\(i,j\)成分をもつ行列のこと。
\begin{align} G_{ij} \overset{i.i.d.}{\sim } N_{\mathbb{C}}(0,1) \hspace{0.3cm}(i,j = 1,2, \cdots ,p) \end{align}
で、\(p \times p\)のGinibreランダム行列のアンサンブルをGinibre(p)とすると、 \( G \sim Ginibre(p)\)に対して、
\begin{align} Z_{\theta} = G\cos\theta + G^\ast \sin\theta \end{align}
と定義する。\(G^\ast\) は\(G\)のエルミート共役。
このとき、\( k \in \mathbb{Z}\) に対して、\( \theta = k \pi /2 \)のときには\(G\)と同分布であり、
\( \theta = ( k + 1/4 ) \pi \)のときに\( Z_{\theta} \)はエルミート行列、すなわちGUEとなる。
ここからが本題で、まずはGの固有値分布に興味がある。
Ginibre(p)の固有値分布
- 複素平面上の半径\( \sqrt{p}\)に一様に分布する
このとき、固有値のほとんどが半径\(\sqrt{p}\)の円内に存在する。したがって固有値の密度は概ね\(1/\pi \)になる。 \( p \rightarrow \infty \)のときにランダムに密度\(1/\pi \)で分布する。これをGinibre点過程という。
以下のような感じ(数セミP27図1に対応)。

import numpy as np import matplotlib.pyplot as plt %matplotlib inline ps = [100, 400, 900] for idx, p in enumerate(ps): Z =np.random.normal(0,1/np.sqrt(2),p*p).reshape(p,p) + 1j*np.random.normal(0,1/np.sqrt(2),p*p).reshape(p,p) ev, _ = np.linalg.eig(Z) axes[idx].scatter(ev.real, ev.imag,s=5) axes[idx].set_title('p=' + str(p)) axes[idx].set_xlabel('Re') axes[idx].set_ylabel('Im') axes[idx].grid(True)
GUE(p)の固有値分布
- GUEの固有値は全て実数
Ginibre行列のときに円内に分布していた固有値が全て実軸上に落ちてくるような感じ(下図左)。 よって原点近傍ほど密度が高くヒストグラムを書くと区間\( [-2\sqrt{p}, 2\sqrt{p}]\)の半円内に分布しているような現象が確認できる。 これが有名なWignerの半円則と呼ばれる現象である(下図右)。 同様に\( p \rightarrow \infty \)のときには実軸上にランダムに分布する。これをsine点過程という。
以下のような感じ(下図の右が数セミP27図2に対応)

p=400 Z =np.random.normal(0,1/np.sqrt(2),p*p).reshape(p,p) + 1j*np.random.normal(0,1/np.sqrt(2),p*p).reshape(p,p) k=1 theta=(k+1/4)*np.pi Z_theta = Z*np.cos(theta) + np.conjugate(Z.T) * np.sin(theta) ev_theta, _ = np.linalg.eig(Z_theta) fig,axes = plt.subplots(nrows=1,ncols=2,figsize=(8,4)) # GUEの固有値の複素平面上の分布 (全て実数固有値なので実軸上に分布) axes[0].scatter(ev_theta.real, ev_theta.imag, s=5) axes[0].set_title('p={}, k={}'.format(p,k)) axes[0].set_xlabel('Re') axes[0].set_ylabel('Im') axes[0].grid(True) # GUEの固有値ヒストグラム axes[1].hist(ev_theta.real, bins=40) axes[1].set_title('p={}, k={}'.format(p,k)) axes[1].set_ylabel('count') axes[1].grid(True)
ちなみに、上記で、
k=1 theta=(k/2)*np.pi
とすると、Ginibre(p)と同じような絵が得られる(下図)。

さらに、
k=0.5 theta=(k+1/4)*np.pi

ランダム性と斥力の関係?
\( p \rightarrow \infty \)の極限におけるランダム性は、前回取り上げた香取さんの記事における固有値間の斥力相互作用の帰結と解釈できるだろうか?
うーん、おもしろい。
次回は白井さんの記事の本題である行列式点過程を理解してまとめてみる。
私からは以上です。
ランダム行列をちょっと勉強してみるテスト
数学セミナーの2019年2月号でランダム行列が特集されていた。

- 出版社/メーカー: 日本評論社
- 発売日: 2019/01/12
- メディア: 雑誌
- この商品を含むブログを見る
ランダム行列は以前から勉強したくて、こちらの本なんかをちら見していたけど、 ちゃんと式などは追っていなくて、現象論的に面白そうだなーというくらいの認識だった。

- 作者: 渡辺澄夫,永尾太郎,樺島祥介,田中利幸,中島伸一
- 出版社/メーカー: 森北出版
- 発売日: 2014/04/17
- メディア: 単行本(ソフトカバー)
- この商品を含むブログを見る
そんなところで今月の数セミを読んでさらに興味がわいた。 余談だが、最近数セミの特集が無双すぎて定期購読再開を検討しているところである。
もちろん頁数制約や一般向け雑誌という性質上、数セミだけを読んでもその数学的な構造はおえないだろうが、 物理や情報の文脈でどういう風に顔を出すかを外観できて非常に興味深い。
そもそもランダム行列とは、確率変数を成分とする行列のことで、そういう行列のアンサンブルを考えたときの統計的性質に興味があるという分野。 特に行列サイズが非常に大きいとき(例えば無限大の極限)での振る舞い(半円則で知られるような固有値分布など)に興味があるようだ。
奇遇である。私も興味がある。 ということでちゃんと勉強していこうという話である。
香取眞理さん(中央大学理工学部)の「ランダム行列とはなにか」でガウシアンユニタリアンサンブル(GUE)が紹介されている。 (余談だが、学部時代(10年以上前)に香取さんの非平衡統計力学 (裳華房テキストシリーズ―物理学)で流体と統計力学の関係を勉強したような気がする。なんかすごくわかりやすかったという記憶があるが、多分わかっていなかったと思う。)
さて、GUEは行列の各成分がi.i.d.なガウシアンに従い、さらにエルミート条件を課したものである。
すると、
の固有値がすべて実数になることが保証されたりと調べやすい対象になるのである。
で、エルミート条件よりのランダム行列
の固有値の確率測度が以下(P.10の(4)式)のように得られる。
\begin{align} P(\boldsymbol{\Lambda} \in d \boldsymbol{\lambda}) = c_2 \exp \left(-\frac{\beta}{4} |\boldsymbol{\lambda}|^2\right) \prod_{1\leq j < k \leq N} (\lambda_k-\lambda_j)^\beta d\boldsymbol{\lambda} \end{align}
上記の導出仮定でのエルミート性を使っている。
\( c_2\)は規格化定数、\( \beta\) は逆温度パラメータ、
\( \mathrm{Tr}X^\dagger X =\sum_{j=1}^N \lambda_j^2 = |\boldsymbol{\lambda}|^2 \)、\( d \boldsymbol{\lambda} = \prod_j^N d\lambda_j\)。
で、これの見方は、\(|\lambda_j - \lambda_k | \rightarrow 0 ( j \neq k)\)とすると、\(P(\boldsymbol{\Lambda} \in d \boldsymbol{\lambda}) \rightarrow 0\)になるので、固有値同士が斥力的な相互作用でランダムに分布している、ということを表している(しゅごい)。
で、これをギブス測度で書き直すとハミルトニアンが \begin{align} \mathcal{H} = \frac{\boldsymbol{|\lambda|}^2}{4} - \sum_{1\leq j < k \leq N} \log(\lambda_k - \lambda_j) \end{align} の格好で出てきて、2体間の相互作用が全固有値間に働き、2体ポテンシャルが常に発散する対数関数になっている。このような系は1次元対数ガス系と呼ぶ。
うーん、めちゃめちゃおもしろい(小並感)。
香取さんの記事はここで終わりではなく、GUEの拡散現象にも言及していて、固有値の時間発展であるダイソン模型を導出している。 GUEの固有値たちの運動方程式なので、上記の1次元対数ガス系を構成する粒子たちの運動方程式ということか。
おもしろすぎてやばい(語彙力)。
確率過程ちゃんと勉強せねばーという気持ちである。
固有値分布の円則は次のポストで適当に実験してみることにする。実験というほどでもないけど…。
私からは以上です。
All-but-the-top: 単語分散表現の上位主成分がノイズな件
Skip-gramやGloVeで学習した単語分散表現に簡単な後処理を施すことで後段タスクの性能を向上させる手法が提案されている。
この論文。論文タイトルが提案手法を一言で表現していて洒落ている。
All-but-the-Top: Simple and Effective Postprocessing for Word Representations
提案手法を一言でいうと,単語分散表現行列を主成分分析して上位主成分を取り除くという超シンプルな方法。 なぜ性能が上がるのかというのは直感的にはよくわからないが,どうも数理的な背景があるらしい。
先行研究において,理想的には任意の単位ベクトルと単語分散表現の内積から計算されるある量(確率モデルの分配関数)が漸近的に定数であるという主張があるが, 実際に学習されたword2vecやGloVeのoff the shelf なモデルはそうなっておらず,本研究でそうなるような後処理をしてみると性能が上がったという話。
もう少し背景を話すと,GloVeやSkip-gramの確率モデルは単語ベクトルとその文脈語の内積をエネルギー関数としてモデル化される。
共起する単語は内積を大きく,すなわち確率を大きくしていくというモデル。
確率モデルの分母の分配関数は学習時に明示的に正規化しない(する必要がない)。
\begin{align} Z(c) = \sum_{w \in V} \exp(c \cdot v(w)) \end{align}
ただ,正規化されているほうが望ましいということのようだ。これを自己正規化というらしい。 要するにこの研究ではそのような自己正規化を誘導するような後処理手法を導出したというお話。 自己正規化具合いを定量評価する指標として,本研究では以下のIsotropyという量を定義している。
\begin{align} I(\{v(w)\}) = \frac{\min_{\|c\|=1} Z(c)}{\max_{\|c\|=1} Z(c)} \end{align}
ここで\(c\)は任意の単位ベクトルである。\(Z(c)\)が\(c\)によらず一定であれば良いのだからIsotropyが1に近いほど良いということになる。 つまり,すでに存在している単語ベクトル空間に対してIsotropyが1になるような後処理を施してやるという戦略である。
のちの実験ではランダム単位ベクトルに対して\(Z(c)\)の分布の形状を後処理前後で比較する(論文中のTable 2, Figure 3)。
ともかく実装してみた。
実装
- wordembeddings.py
GloVeのモデルをロードするクラス
import numpy as np from tqdm import tqdm class WordEmbeddings(): def __init__(self, path='glove.6B.100d.txt'): self.word2vec = {} with open(path) as f: for line in tqdm(f): values = line.split() word = values[0] vec = np.asarray(values[1:], dtype='float64') self.word2vec[word] = vec def get_embeddings_matrix(self): embeddings_matrix = np.stack(list(self.word2vec.values())) return embeddings_matrix
- 単位超球上の一様分布
こちらから拝借しました。ありがとうございます。
def sample_spherical(npoints, ndim): vec = np.random.randn(ndim, npoints) vec /= np.linalg.norm(vec, axis=0) return vec.T # (npoint, dimen)
- All-but-the-top の本体
def abtt(): dimen = 50 # dimensions for Word Embeddings D = 2 # number of the removed directions c = sample_spherical(npoints=100, ndim=dimen) # random unit vectors wordemb = wordembeddings.WordEmbeddings(path='glove.6B.{}d.txt'.format(dimen)) V = wordemb.get_embeddings_matrix() Z_before = (np.exp(c @ V.T)).mean(axis=1) print('Isotropy(before) : ', np.abs(Z_before.min()/Z_before.max())) mu = np.mean(V, axis=0) V_tilde = V - mu # centering pca = PCA(n_components=D) pca.fit(V_tilde) coef = pca.components_ @ V_tilde.T diff = coef.T @ pca.components_ V_prime = V_tilde - diff Z_af = (np.exp(c @ V_prime.T)).mean(axis=1) print('Isotropy(after) : ', np.abs(Z_af.min()/Z_af.max())) lower = np.concatenate([Z_before, Z_af]).min() - 0.2 upper = np.concatenate([Z_before, Z_af]).max() + 0.2 bins = np.linspace(lower, upper, 50) plt.hist(Z_before, bins, alpha = 0.5, label='before') plt.hist(Z_af, bins, alpha = 0.5, label='after') plt.legend() plt.xlabel('Z(c)') plt.ylabel('frequency') # plt.savefig('abtt.png', bbox_inches='tight') # plt.show()
実験
ここでは前処理前後でのIsotropyの変化をみる。論文中のTable 2, Figure 3に対応する。使った分散表現のモデルはここから入手できるGloVeの最も小さいモデル(6B.zipの50次元)。
論文で使用されたGloVeは大きいモデル(ファイルサイズ数GB)だが, 傾向を観るだけなら小さいモデルでも十分であったためそうした。
結果
- Isotropyの値(論文中のTable2に相当)
- Isotropy(before) : 0.36
- Isotropy(after) : 0.92
前処理前後で1に漸近していることがわかる。
- Z(c)の分布(論文中のFigure 3に相当)
前処理前後で\(Z(c)\)が\(c\)によらず定数になっていることがわかる。概ね傾向としては論文と同様。 これはIsotropy→1を意味する。
私からは以上です。
ポアソン混合モデルのギブスサンプリング
以下の本の4章を実装していく。

機械学習スタートアップシリーズ ベイズ推論による機械学習入門 (KS情報科学専門書)
- 作者: 須山敦志,杉山将
- 出版社/メーカー: 講談社
- 発売日: 2017/10/21
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (1件) を見る
まずはギブスサンプリングから。
設定
問題設定としては、観測データの生成過程にポアソン混合モデルを仮定して、
その混合要素である各ポアソン分布のパラメータと混合比
の分布が知りたい。
アルゴリズム
ギブスサンプリングのアルゴリズムの導出は、上記教科書に丁寧にかかれているので省略。 結論はP.133 のアルゴリズム4.2にまとめられている。結論のみ書いておく。

実験
コードは末尾にある。
まずは疑似データを生成する。
疑似データは、観測量の数N= 1000とし、
がそれぞれ5,20,50の3つのポアソン分布(k=3)から生成されているとする。
混合比は適当に3:6:1とした。
以下の観測量のヒストグラム。

以下が、MAXITER=100で実験したときの iter 20 刻みの状況。青が観測量、赤が予測。
iter=40辺りで多峰性(ここでは3)を捉えている。
まぁそもそも簡単なデータなので、だからどうしたという感じではあるが。






コード
numpy で実装した。
import numpy as np def fit(X, k, maxiter=100): N = X.shape[0] # hyperparams lambda_k = np.random.rand(k) pi_k = np.random.rand(k) a_ini = np.random.rand() b_ini = np.random.rand() alpha_k_ini = np.random.rand(k) pred_history = [] for _iter in range(maxiter): # sample s_n from Categorical dist. eta_nk = np.exp(np.outer(X, np.log(lambda_k)) - lambda_k + np.log(pi_k)) z = np.linalg.norm(eta_nk, ord=1, axis=1) eta_nk = eta_nk / z[:, np.newaxis] s_n = np.empty((N, k)) for n in range(N): s_n[n] = np.random.multinomial(n=1, pvals=eta_nk[n]) # sample lambda_k from Gamma dist. a_hat = s_n.T@X + a_ini b_hat = s_n.sum(axis=0) + b_ini lambda_k = np.random.gamma(shape=a_hat, scale=1./b_hat) # Sample pi_k from Dirichlet dist. alpha_hat = s_n.sum(axis=0) + alpha_k_ini pi_k = np.random.dirichlet(alpha_hat) if _iter == maxiter - 1 or _iter % 20 == 0: pred_history.append((lambda_k.copy(), pi_k.copy())) return pred_history
import matplotlib.pyplot as plt p0 = np.random.poisson(5, 300) p1 = np.random.poisson(20, 600) p2 = np.random.poisson(50, 100) X = np.hstack((p0,p1,p2)) plt.hist(X, bins=20) plt.show() pred_his = fit(X, k=3)
余談 ガンマ分布の定義
須山本と numpy.random.gamma におけるパラメータの表現が少し異なるため、APIを使う時には注意が必要。以下の定義を見比べてみると明らかなように、須山本のa、b は numpy.random.gamma のキーワード引数shape (k)とscale(
)にそれぞれ対応している。
須山本の定義は式2.46で与えられていて、次式。
-
一方 numpy.random.gamma は 次式
以上です。
次回は変分推論を実装します。
非負値行列分解で画像圧縮
非負値行列因子分解というものがある。 Non-negative matrix factorization、NMFとよばれる。
Lee and Seung, nature 1999
http://www.columbia.edu/~jwp2128/Teaching/E4903/papers/nmf_nature.pdf
そもそも行列分解というのは、任意の行列に対して
しばしば低ランク性を仮定して、2つの行列
の積で近似しようというもの。
分解の仕方はいろいろあるが、特異値分解(SVD)がたぶん有名なやつ。主成分分析(PCA)と本質的には同じ。
コスト関数はいろいろあるけど、VとWHの差のフロベニウスノルム。 (ベイズ的解釈でpriorに何選ぶかが関係しているが、それはまた別の記事で)
で、非負値行列分解とは、の要素がそもそも非負ってわかってるなら、
分解するときにその制約入れたほうが良いよねという発想。だから非負値っていう。そのままやな。つまり上記の場合は以下の最小化問題を解くことになる。
となる。
アルゴリズムはいろいろあるらしいが簡単なやつがあって、 Multiplicative update rulesって呼ばれるアルゴリズムが下記論文で提案されたうちの一つ。
Daniel D. Lee, H. Sebastian Seung, Algorithms for Non-negative Matrix Factorization, NIPS2000
https://papers.nips.cc/paper/1861-algorithms-for-non-negative-matrix-factorization
乗法更新法の更新則は以下(上記論文の式(4))。これを適当な回数イテレートすればオッケ。
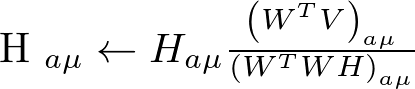
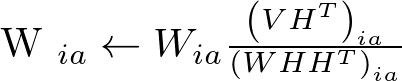
上記をnumpyで愚直に実装しmnistの画像を圧縮してみた。コードは最後にはりつけた。
ちなみに、現在mldata.orgの鯖が落ちてるらしいので、 以下のように直接ダウンロードしてfetch_mldataのfetch先をローカルキャッシュしておく*1。
$ mkdir -p ~/scikit_learn_data/mldata && cd $_ $ wget https://github.com/amplab/datascience-sp14/raw/master/lab7/mldata/mnist-original.mat
参考
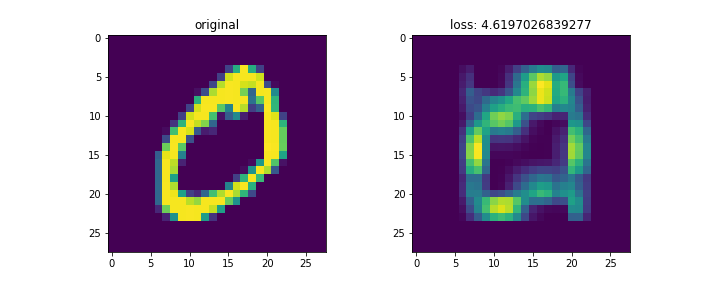
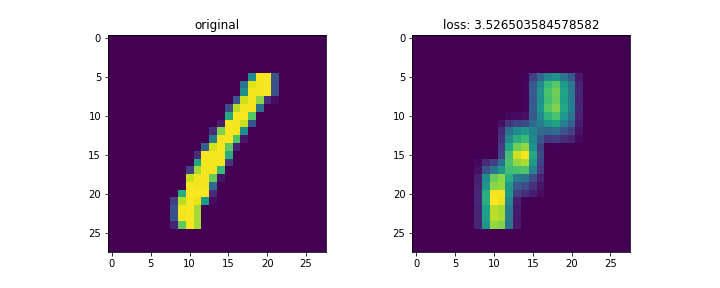
結果は以下。
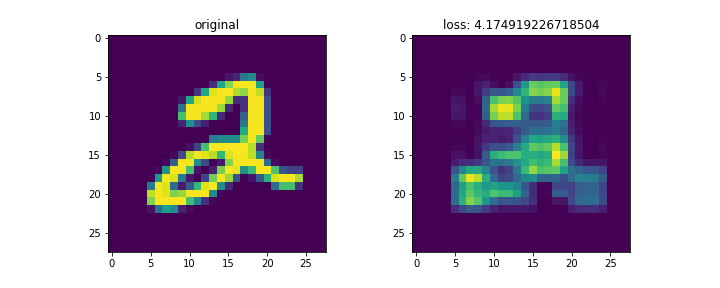
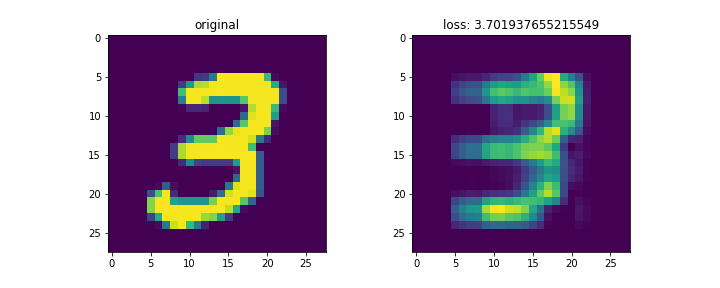
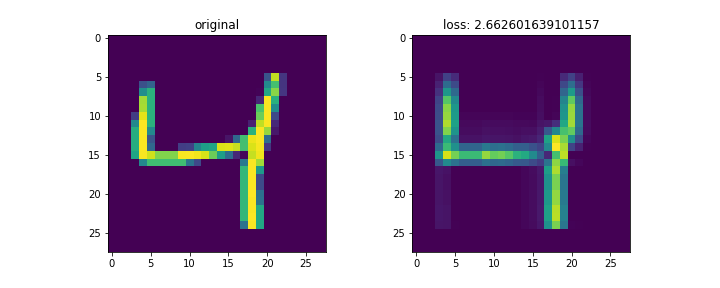
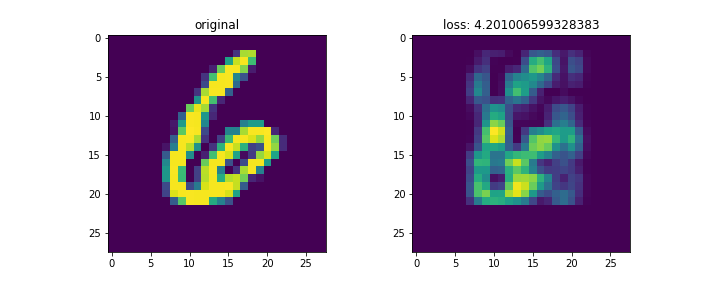
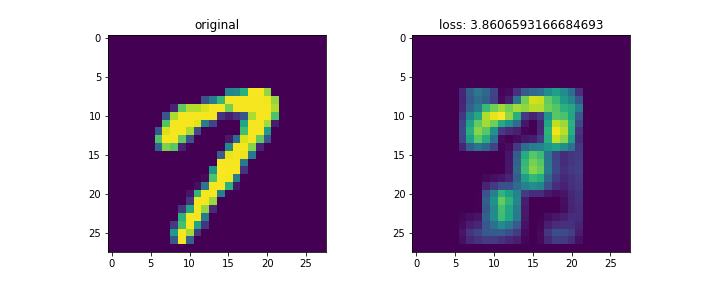
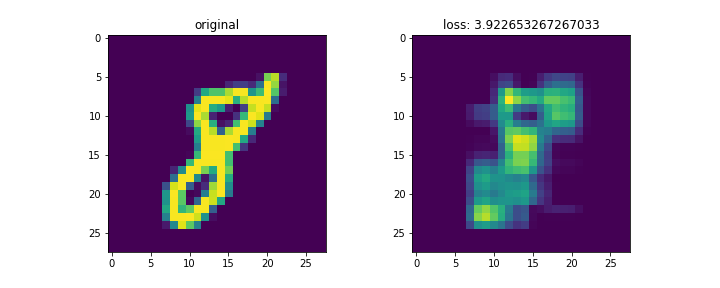
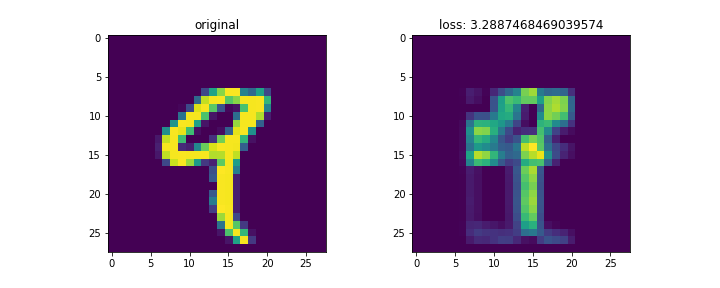
mnistは28x28の画像。これをランク3で分解して再構成した。
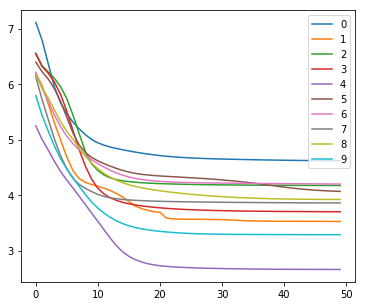
左列が元画像、右列が復元画像。末尾の画像はイテレーションに対する数字別のロスの変化。
画像によってnnz数が異なるため、画像ごとのロスを単純に比較するのはあまり意味がないと思われる。

コードは以下。
import numpy as np from sklearn.datasets import fetch_mldata import matplotlib.pyplot as plt mnist = fetch_mldata('MNIST original') X, y = mnist.data, mnist.target X = X/255. target_num = [] for i in range(10): idxs = np.where(y == i) idx = np.squeeze(idxs)[0] target_num.append(idx) loss_t = [] for num_label, idx in enumerate(target_num): fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(10,4)) r = 3 V = X[idx,:].reshape(28,28) (m,n) = V.shape[0:2] ax1.imshow(V) ax1.set_title('original') W = np.random.rand(m,r) H = np.random.rand(r,n) local_loss = [] for i in range(50): H = H * ((W.T@V)/(W.T@W@H)) H[np.isnan(H)] = 0. W = W *((V@H.T)/(W@H@H.T)) W[np.isnan(W)] = 0. loss = np.linalg.norm(V - W@H, 'fro') local_loss.append(loss) loss_t.append(local_loss) ax2.imshow(W@H) ax2.set_title('loss: {}'.format(loss)) fig.show() plt.clf() fig = plt.figure(figsize=(6,5)) for i, _loss in enumerate(loss_t): plt.plot(_loss, label=str(i)) plt.legend() plt.show()